3. Theory of Sets
🔷 সেট তত্ত্ব
জার্মান গণিতবিদ জর্জ ক্যান্টর (১৮৪৫-১৯১৮) সেট সম্পর্কে প্রথম ব্যাখ্যা প্রদান করেন। তিনি অসীম সেটের ধারণা প্রদান করে গণিতশাস্ত্রে আলোড়ন সৃষ্টি করেন এবং তার সেটের ধারণা সেট তত্ত্ব (Set Theory) নামে পরিচিত।
🔷 সেট কী বা সেট কাকে বলে
বাস্তব বা চিন্তাজগতের সু-সংজ্ঞায়িত বস্তুসমূহের সমাবেশ বা সংগ্রহকে ইংরেজিতে “সেট” (Set)। সহজ করে বলা যায়, একই জাতীয় বস্তুর সমষ্টি হল “সেট” (Set) বলে। যেমন: অনার্স দ্বিতীয় বর্ষের ছাত্র-ছাত্রীদের সেট, ঢাকা কলেজের সকল শিক্ষকদের সেট, প্রথম দশটি বিজোড় সংখ্যার সেট, পূর্ণ সংখ্যার সেট, বাস্তব সংখ্যার সেট ইত্যাদি।
🔶 সেটের উপাদান
যেসকল বস্তু নিয়ে সেট গঠিত, তাদেরকে ঐ সেটের উপাদান বা সদস্য বলা হয়। সেটের প্রত্যেক বস্তু বা সদস্যকে সেটের উপাদান (elements of set) বলা হয়। সেটের উপাদানগুলোকে সাধারণত কমা (,) দ্বারা আলাদা করা হয়। সেট প্রকাশের জন্য ইংরেজি বড় হাতের অক্ষর (যেমন- A,B,C…..X, Y, Z) ব্যবহার করা হয়। সেট প্রকাশের জন্য সবসময় দ্বিতীয় বন্ধনী ({} ) ব্যবহার করা। কোনো সেটের উপাদানকে ‘∈’ (Belongs to) দ্বারা প্রকাশ করা হয়। আর সেটের উপাদান নয় বুঝাতে ‘∉’ (Not belongs to) ব্যবহার করা হয়।

সেট হবার শর্ত দুটি হচ্ছে-
১। সুনির্দিষ্টতা হওয়াঃ উপাদান সমূহের মধ্যে যে কোন ভাবে একটা মিল থাকবে।
২। সু-সংজ্ঞায়িত হওয়াঃ অস্পষ্ট উপাদান বা মতভেদ আছে এমন তথ্য সেট নয়।
জেনে রাখা ভাল (বিশেষ সংখ্যা সেট)
১। সকল স্বাভাবিক সেট হচ্ছে N: সকল স্বাভাবিক সংখ্যার সেট কে N দ্বারা প্রকাশ করা হয়।
যেমন, N = {0, 1, -1, 2, -2, 3, -3, …}
২। বাস্তব সংখ্যার সেট হচ্ছে R: সকল মূলদ ও অমূলদ সংখ্যার সেট কে R দ্বারা প্রকাশ করা হয়।
যেমন, R = { 2, -3.14, 2.71828, …}
৩। পূর্ণসংখ্যার সেট সংখ্যা হচ্ছে Z:
সকল পূর্ণসংখ্যা, ধনাত্মক এবং ঋণাত্মক উভয়কেই Z দ্বারা প্রকাশ করা হয়।
যেমন, Z = {…, -3, -2, -1, 0, 1, 2, 3, …}
৪। ভগ্নাংশ সহ সকল বাস্তব সংখ্যার সেট হচ্ছে Q:
ভগ্নাংশ সহ সকল বাস্তব সংখ্যার সেটকে Q দ্বারা প্রকাশ করা হয়।
যেমন, Q = {1/2, -3/4, 0.333, …}
৫। কমপ্লেক্স সংখ্যার সেট হচ্ছে C:
ঋনাত্মক বা ধনাত্মক সকল জটিল সংখ্যার সেটকে C দ্বারা প্রকাশ করা হয়।
যেমন, C = { 2 + 3i, -1 – 4i, …}
সেট প্রকাশের পদ্ধতি –
১। তালিকা পদ্ধতি
২। সেট গঠন পদ্ধতি
তালিকা পদ্ধতিঃ সেটের সকল উপাদান সুনির্দিষ্টভাবে উল্লেখ করে দ্বিতীয় বন্ধনীর ‘{ }’ মাধ্যমে প্রকাশ করা হয় এবং একাধিক উপাদানকে ‘ কমা’ এর মাধ্যমে আলাদা করা হয়।
যেমন, M={a,b,c} ,B={2,3, 4, 5} ইত্যাদি।
সেট গঠন পদ্ধতিঃ সেট গঠন পদ্ধতি সেটের সকল উপাদান সুনির্দিষ্টভাবে উল্লেখ না করে উপাদান নির্ধারণের জন্য সাধারণ ধর্ম বা গঠনের উল্লেখ থাকে।
যেমন: A={x:x স্বাভাবিক জোড় সংখ্যা}, B={x:x 2 এর গুণিতক}
এখানে ‘:’ (such that) চিহ্ন দিয়ে ‘এরূপ যেন’ বা ‘যেন ‘বোঝায়। এ পদ্ধতিতে সেটের উপাদান নির্ধারণের জন্য শর্ত বা rule দেওয়া থাকে তাই এই পদ্ধতিকে “Rule method ” বলা হয়।
সেটের সংজ্ঞা উদাহরণ সহ
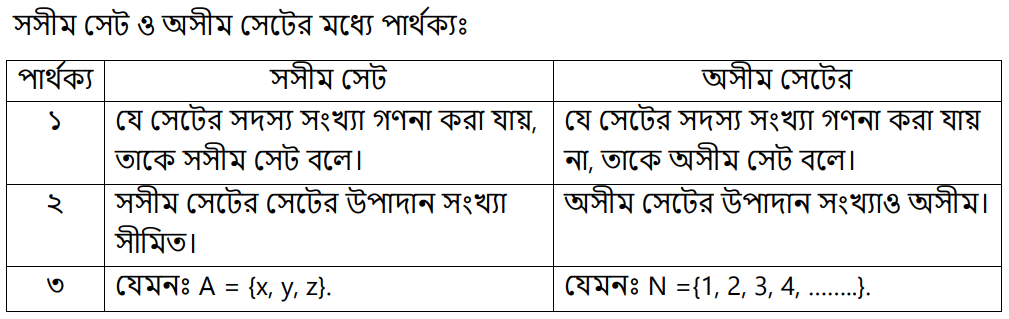
সসীম সেট (Finite Set) : যে সেটের উপাদান সংখ্যা গণনা করে নির্ধারণ করা যায়, একে সমীম সেট বলে। যেমন, D = {x, y, z}, E = {3, 6, 9,……..,60}।
অসীম সেট (Infinite Set) : যে সেটের উপাদান সংখ্যা গণনা করে নির্ধারণ করা যায় না, একে অসীম সেট বলে। যেমন, A = {x : x বিজোড় স্বাভাবিক সংখ্যা}, স্বাভাবিক সংখ্যার সেট N ={1, 2, 3, 4, ……..}, পূর্ণসংখ্যার সেট Z = {…….-3, – 2, -1, 0,1, 2, 3…….}, মূলদ সংখ্যার সেট Q = {p/q : p ও q পূর্ণ সংখ্যা এবং q ≠ 0}, বাস্তব সংখ্যার সেট R ইত্যাদি অসীম সেট।
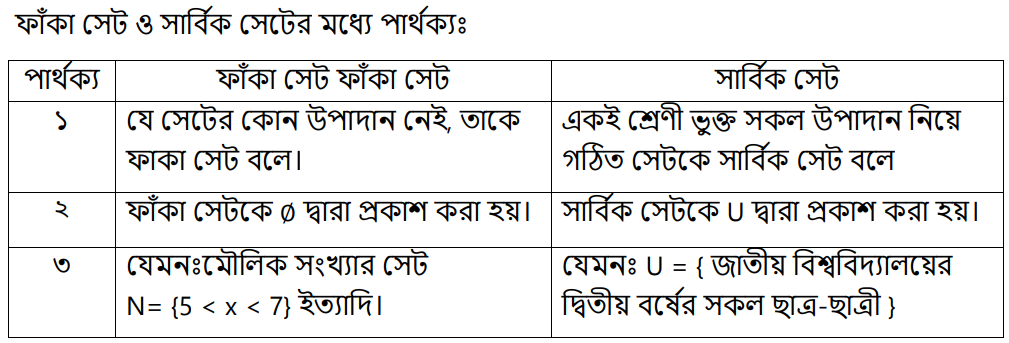
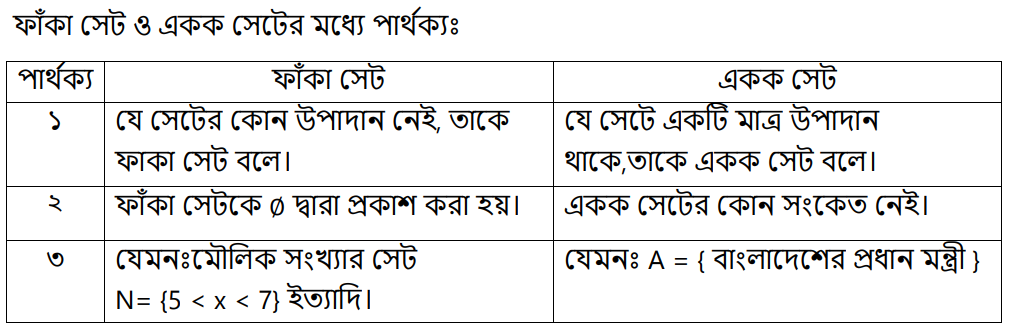
ফাঁকা সেট (Empty Set) : যে সেটের কোনো উপাদান নেই একে ফাঁকা সেট বলে। ফাঁকা সেটকে ∅ দ্বারা প্রকাশ করা হয়। যেমন : হলিক্রস স্কুলের তিনজন ছাত্রের সেট, {x ∈ N :10 < x < 11}, {x ∈ N : x মৌলিক সংখ্যা এবং 23 < x < 29} ইত্যাদি।
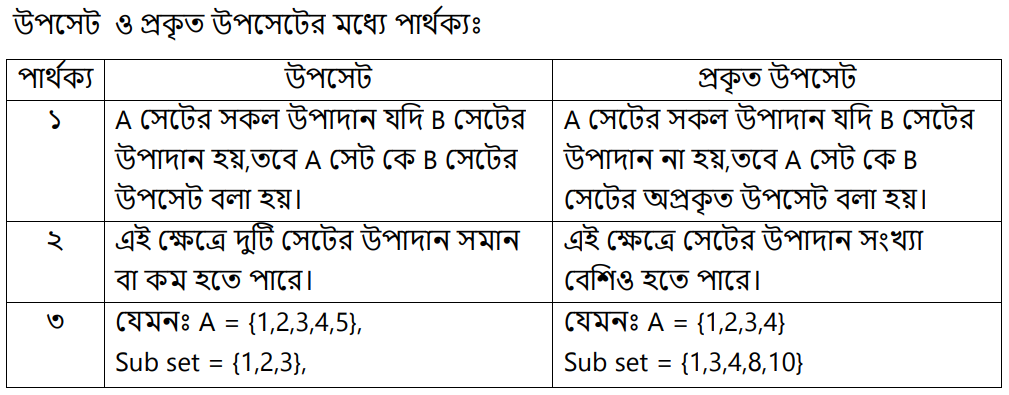
উপসেট (Subset) : A = {a, b} একটি সেট। A সেটের উপাদান থেকে {a, b}, {a }, { b} সেটগুলো গঠন করা যায়। আবার, কোনো উপাদান না নিয়ে Φ সেট গঠন কর যায়।
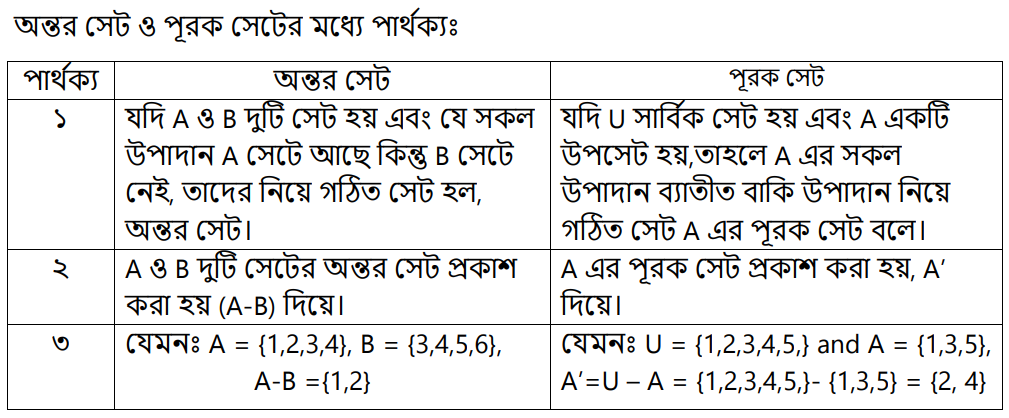
সেটের অন্তর (Difference of Set) : মনে করি, A = {1, 2, 3, 4, 5} এবং B = {3, 5}| সেট A থেকে সেট B এর উপাদানগুলো বাদ দিলে যে সেটটি হয় তা {1, 2, 4} এবং লেখা হয় A \ B বা A – B = {1, 2, 3, 4, 5} – {3, 5} = {1, 2, 4}
সুতরাং, কোনো সেট থেকে অন্য একটি সেট বাদ দিলে যে সেট গঠিত হয় তাকে বাদ সেট বলে।
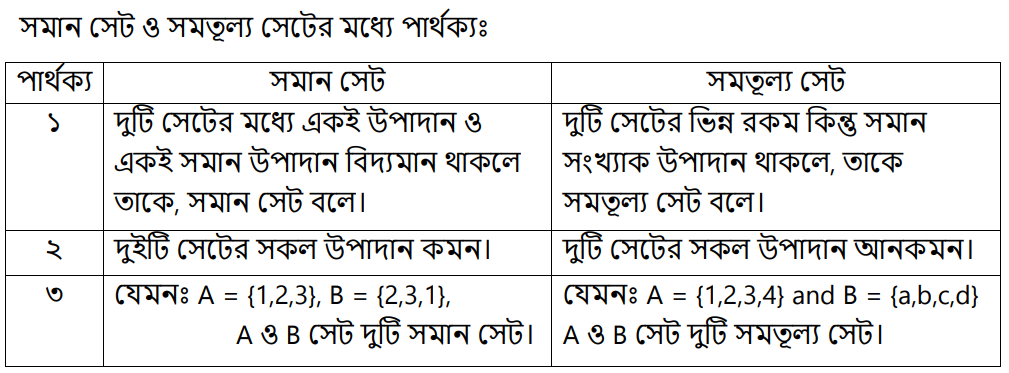
সমতুল্য সেট (Equivalent set) : দুটি সেটের উপাদান ভিন্ন হলেও উপাদান সংখ্যা সমান হলে, তাকে সমতুল্য সেট বলে। যেমনঃ A = {1,2,3} B = {a,b,c}
অ-প্রকৃত উপসেট (Improper subset) : A সেট এর সকল উপাদান যদি B সেটে থাকে বা তারও বেশি থাকে, অ-প্রকৃত উপসেট বলে। যেমনঃ A = {1,2,3} improper subset, B = {1, 2, 5}
প্রতি সম অন্তর সেট (Symmetric difference set) : দুটি সেটের অধিকাংশ উপাদান একই থাকার পরেও, ১টি উপাদান ১ম সেটে আছে, দ্বিতীয় সেটে নাই আবার, ১টি উপাদান দ্বিতীয় সেটে আছে, কিন্তু ১ম সেটে নাই, তাকে প্রতি সম অন্তর সেট বলে। যেমনঃ A = {1,2,3,4,5} B = {0,1, 2, 3, 4}
শক্তিসেট (Power set) : কোন সেটের সকল উপসেট নিয়ে গঠিত সেটকে শক্তি সেট বলে। যেমনঃ A = {1,2} power set of A = {1}, {2}, {1,2}, { }
সার্বিকসেট (Universal set) : একই শ্রেণী ভুক্ত সকল উপাদান নিয়ে গঠিত সেটকে সার্বিক/ সার্বজনীন সেট বলে। সার্বিক সেটকে U দ্বারা প্রকাশ করা হয়। যেমনঃ U = { জাতীয় বিশ্ববিদ্যালয়ের দ্বিতীয় বর্ষের সকল ছাত্র-ছাত্রী }
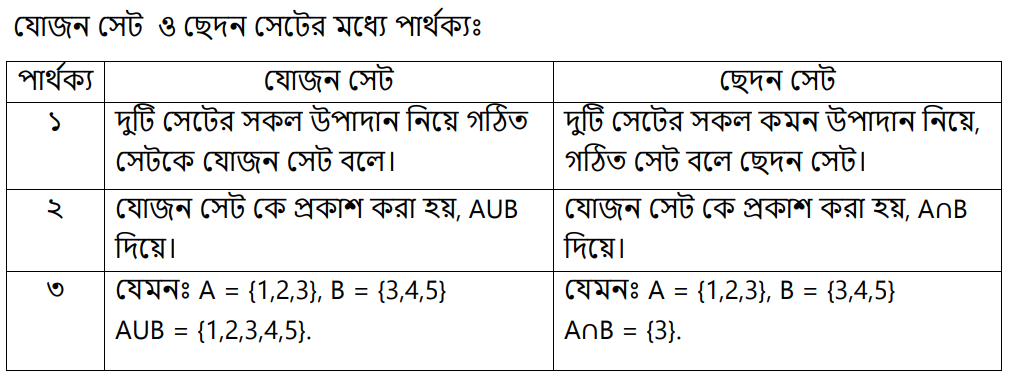
বিভিন্ন প্রকার সেটের মধ্যে পার্থক্য
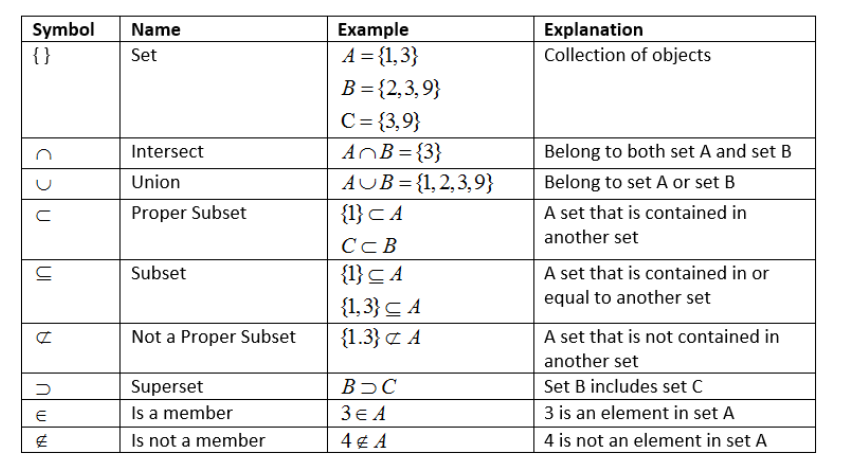
Symbol of set
Part-A with solution
Lorem ipsum dolor sit amet, consectetur adipiscing elit. Ut elit tellus, luctus nec ullamcorper mattis, pulvinar dapibus leo. Lorem ipsum dolor sit amet, consectetur adipiscing elit. Ut elit tellus, luctus nec ullamcorper mattis, pulvinar dapibus leo.

Video Lesson on What are Sets
Problem:01: In a country the total number of people 50,000 out of them 56% read Ittafaq, 46% Jonokunto and 12% do not read any newspaper.
Require: (a) How many people read both paper (b) How many people read only Ittafaq.(c) Read jonokunto but not ittafaq. (d) Only one paper.


Necessary links